Graphing Linear Functions Answer Key
Learning Outcomes
- Graph a linear function by plotting points
- Graph a linear function using the slope and y-intercept
- Graph a linear part using transformations
We previously saw that that the graph of a linear function is a direct line. We were also able to encounter the points of the function equally well equally the initial value from a graph.
There are three basic methods of graphing linear functions. The first is by plotting points and and so drawing a line through the points. The 2nd is by using the y-intercept and slope. The tertiary is applying transformations to the identity function [latex]f\left(x\correct)=10[/latex].
Graphing a Function by Plotting Points
To detect points of a role, we tin choose input values, evaluate the office at these input values, and calculate output values. The input values and corresponding output values course coordinate pairs. We then plot the coordinate pairs on a grid. In full general nosotros should evaluate the part at a minimum of two inputs in social club to observe at least ii points on the graph of the function. For example, given the function [latex]f\left(x\right)=2x[/latex], nosotros might use the input values 1 and 2. Evaluating the function for an input value of 1 yields an output value of 2 which is represented by the signal (one, 2). Evaluating the role for an input value of 2 yields an output value of four which is represented by the point (2, iv). Choosing three points is often advisable considering if all three points do non fall on the aforementioned line, nosotros know we made an error.
How To: Given a linear part, graph by plotting points.
- Cull a minimum of two input values.
- Evaluate the function at each input value.
- Utilise the resulting output values to place coordinate pairs.
- Plot the coordinate pairs on a grid.
- Describe a line through the points.
Example: Graphing by Plotting Points
Graph [latex]f\left(x\right)=-\frac{two}{3}10+five[/latex] by plotting points.
Attempt Information technology
Graph [latex]f\left(x\correct)=-\frac{iii}{iv}x+6[/latex] by plotting points.
Graphing a Linear Function Using y-intercept and Slope
Another way to graph linear functions is by using specific characteristics of the function rather than plotting points. The first characteristic is its y-intercept which is the indicate at which the input value is zero. To notice the y-intercept, nosotros can gear up [latex]x=0[/latex] in the equation.
The other characteristic of the linear function is its slope,yard, which is a measure of its steepness. Think that the gradient is the rate of modify of the role. The slope of a linear function is equal to the ratio of the alter in outputs to the alter in inputs. Another way to call up about the gradient is by dividing the vertical difference, or ascent, between any two points by the horizontal difference, or run. The slope of a linear function will be the same between any two points. We encountered both the y-intercept and the slope in Linear Functions.
Let's consider the following function.
[latex]f\left(x\correct)=\frac{1}{two}x+i[/latex]
The slope is [latex]\frac{1}{ii}[/latex]. Because the gradient is positive, nosotros know the graph will slant upward from left to correct. The y-intercept is the point on the graph when x= 0. The graph crosses the y-centrality at (0, i). Now we know the gradient and the y-intercept. We can begin graphing by plotting the betoken (0, 1) Nosotros know that the slope is ascension over run, [latex]m=\frac{\text{rise}}{\text{run}}[/latex]. From our example, we have [latex]m=\frac{1}{2}[/latex], which means that the rise is 1 and the run is 2. Starting from our y-intercept (0, ane), we can ascension one and then run two or run 2 and and then ascension ane. Nosotros repeat until we have multiple points, and then we depict a line through the points every bit shown beneath.

A General Note: Graphical Interpretation of a Linear Part
In the equation [latex]f\left(ten\right)=mx+b[/latex]
- b is the y-intercept of the graph and indicates the point (0, b) at which the graph crosses the y-axis.
- m is the slope of the line and indicates the vertical displacement (ascent) and horizontal displacement (run) betwixt each successive pair of points. Think the formula for the gradient:
[latex]m=\frac{\text{alter in output (rising)}}{\text{modify in input (run)}}=\frac{\Delta y}{\Delta 10}=\frac{{y}_{2}-{y}_{i}}{{x}_{2}-{ten}_{1}}[/latex]
Q & A
Do all linear functions have y-intercepts?
Yeah. All linear functions cross the y-axis and therefore accept y-intercepts. (Note: A vertical line parallel to the y-axis does not have a y-intercept. Keep in mind that a vertical line is the simply line that is not a office.)
How To: Given the equation for a linear function, graph the office using the y-intercept and slope.
- Evaluate the role at an input value of zero to find the y-intercept.
- Identify the slope.
- Plot the point represented past the y-intercept.
- Utilise [latex]\frac{\text{rising}}{\text{run}}[/latex] to decide at least two more points on the line.
- Draw a line which passes through the points.
Case: Graphing by Using the y-intercept and Slope
Graph [latex]f\left(x\right)=-\frac{two}{3}10+v[/latex] using the y-intercept and slope.
Endeavor It
Observe a point on the graph nosotros drew in Case: Graphing by Using the y-intercept and Gradient that has a negative x-value.
Show Solution
Possible answers include [latex]\left(-three,vii\right)[/latex], [latex]\left(-six,9\right)[/latex], or [latex]\left(-9,11\correct)[/latex].
Graphing a Linear Function Using Transformations
Some other option for graphing is to use transformations on the identity function [latex]f\left(x\right)=10[/latex]. A function may exist transformed past a shift up, down, left, or right. A function may also exist transformed using a reflection, stretch, or pinch.
Vertical Stretch or Compression
In the equation [latex]f\left(x\correct)=mx[/latex], the one thousand is interim as the vertical stretch or compression of the identity office. When thousand is negative, there is too a vertical reflection of the graph. Notice that multiplying the equation [latex]f\left(x\right)=x[/latex] by g stretches the graph of f past a cistron of thousand units if m> 1 and compresses the graph of f by a cistron of m units if 0 < m< 1. This means the larger the absolute value of m, the steeper the slope.
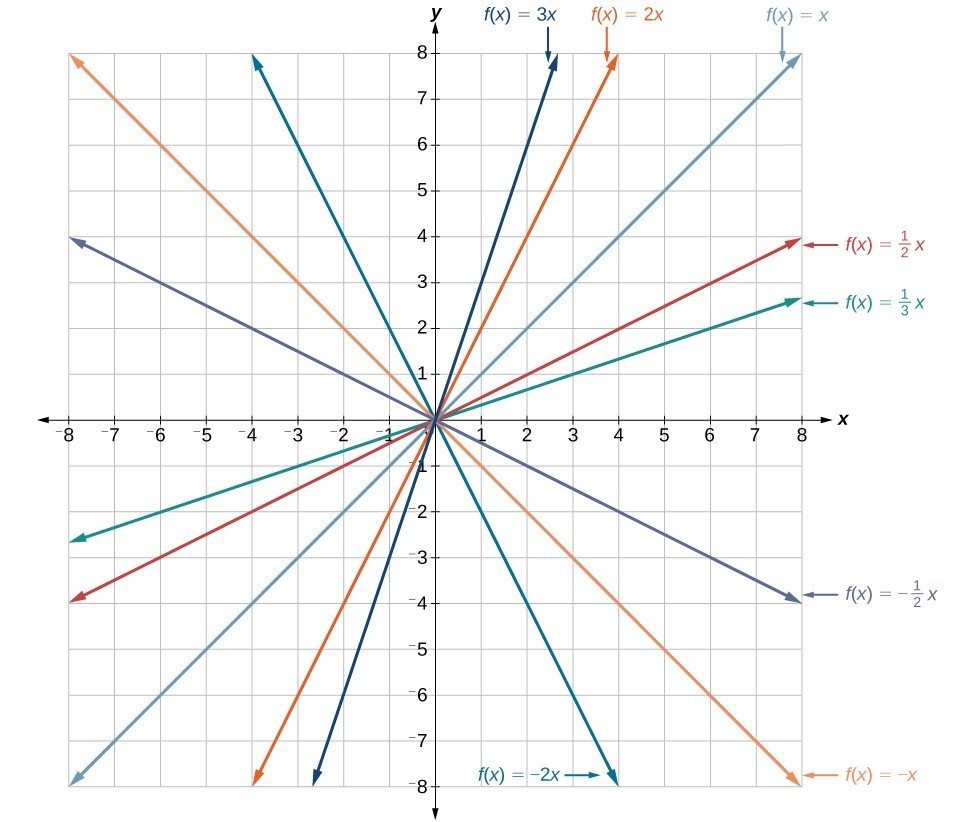
Vertical stretches and compressions and reflections on the function [latex]f\left(x\right)=x[/latex].
Vertical Shift
In [latex]f\left(ten\right)=mx+b[/latex], the b acts equally the vertical shift, moving the graph up and down without affecting the slope of the line. Notice that adding a value of b to the equation of [latex]f\left(x\right)=10[/latex] shifts the graph off a full of b units upwardly if b is positive and |b| units downwards if b is negative.
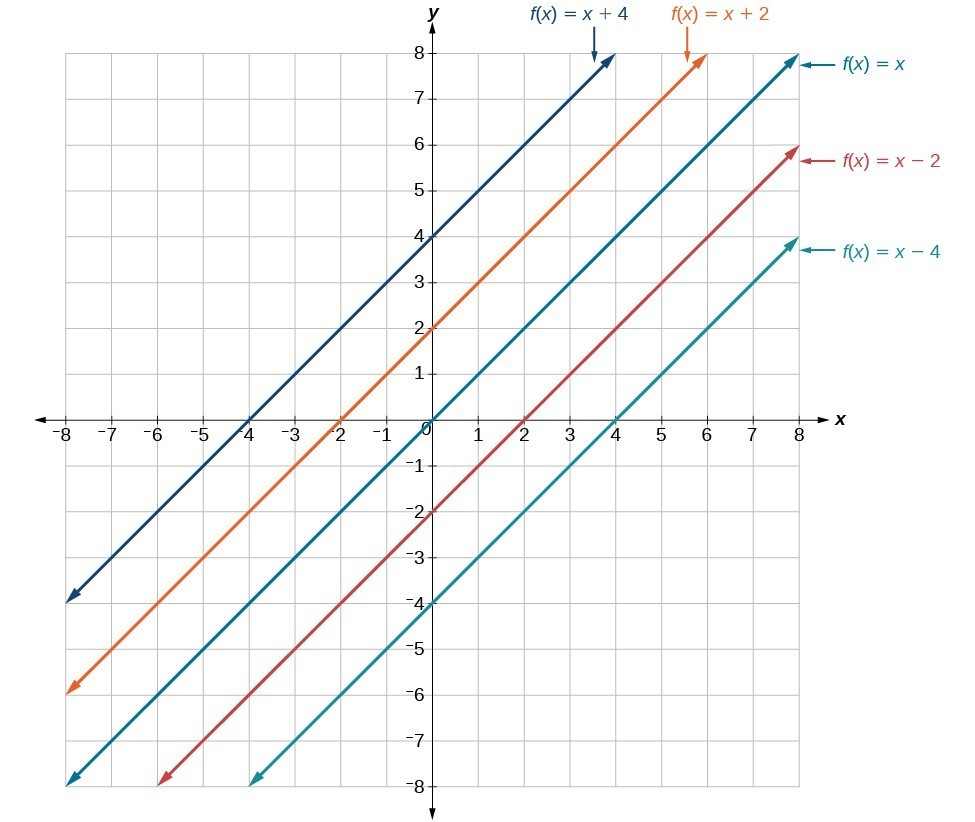
This graph illustrates vertical shifts of the part [latex]f\left(x\right)=x[/latex].
Using vertical stretches or compressions along with vertical shifts is another way to look at identifying dissimilar types of linear functions. Although this may not be the easiest style to graph this type of function, it is all the same of import to exercise each method.
How To: Given the equation of a linear part, use transformations to graph the linear function in the form [latex]f\left(ten\right)=mx+b[/latex].
- Graph [latex]f\left(x\correct)=ten[/latex].
- Vertically stretch or compress the graph by a gene grand.
- Shift the graph up or down b units.
Case: Graphing past Using Transformations
Graph [latex]f\left(x\correct)=\frac{1}{ii}x - three[/latex] using transformations.
Attempt It
Graph [latex]f\left(x\right)=4+2x[/latex], using transformations.
Show Solution

Q & A
In Example: Graphing by Using Transformations, could we take sketched the graph by reversing the lodge of the transformations?
No. The order of the transformations follows the order of operations. When the function is evaluated at a given input, the corresponding output is calculated by post-obit the club of operations. This is why we performed the compression first. For example, following order of operations, let the input be 2.
[latex]\begin{array}{l}f\text{(2)}=\frac{\text{1}}{\text{two}}\text{(two)}-\text{three}\hfill \\ =\text{1}-\text{3}\hfill \\ =-\text{2}\hfill \terminate{array}[/latex]
Contribute!
Did you have an thought for improving this content? We'd beloved your input.
Improve this pageLearn More
Graphing Linear Functions Answer Key,
Source: https://courses.lumenlearning.com/waymakercollegealgebra/chapter/graph-linear-functions/
Posted by: minterolank1963.blogspot.com


0 Response to "Graphing Linear Functions Answer Key"
Post a Comment